A Equação de Bernoulli: Aplicações e Princípios: Exemplo Da Aplicação Da Equação De Bernoulii Principais Fisicos Envolvidos
Exemplo Da Aplicação Da Equação De Bernoulii Principais Fisicos Envolvidos – A equação de Bernoulli é uma ferramenta fundamental na mecânica dos fluidos, descrevendo o comportamento de fluidos em movimento. Ela relaciona a pressão, a velocidade e a altura de um fluido em diferentes pontos de um sistema, assumindo certas simplificações. Este artigo explorará a equação, suas aplicações, limitações e os principais cientistas envolvidos em seu desenvolvimento.
Introdução à Equação de Bernoulli, Exemplo Da Aplicação Da Equação De Bernoulii Principais Fisicos Envolvidos
A equação de Bernoulli, em sua forma mais simples, é expressa como:
P + 1/2ρv² + ρgh = constante
onde P representa a pressão estática, ρ a densidade do fluido, v a velocidade do fluido, g a aceleração da gravidade e h a altura. A equação expressa a conservação de energia em um fluido em movimento. A energia total do fluido, composta pela energia de pressão, energia cinética e energia potencial gravitacional, permanece constante ao longo de uma linha de corrente, desde que certas hipóteses sejam atendidas.
Os princípios físicos subjacentes à equação são a conservação de energia e a conservação de massa. A equação assume um fluxo ideal, ou seja, sem viscosidade, incompressível e sem atrito. Essas hipóteses simplificadoras permitem a aplicação da equação em diversos contextos, embora sua precisão possa ser afetada em situações reais onde essas hipóteses não são totalmente válidas.
Aplicações da Equação de Bernoulli em diferentes contextos
A equação de Bernoulli encontra aplicações em diversos campos da engenharia e da física. Sua utilidade se estende de sistemas hidráulicos a aerodinâmica, permitindo a análise e o projeto de uma ampla gama de sistemas.
| Sistema | Descrição | Variáveis envolvidas | Resultado |
|---|---|---|---|
| Sistema de irrigação | Distribuição de água em uma plantação. | Pressão, velocidade, altura da água em diferentes pontos do sistema de tubulação. | Cálculo do fluxo de água necessário para irrigar a plantação de forma eficiente. |
| Atuador hidráulico | Cilindro hidráulico que move uma carga. | Pressão no fluido, área do pistão, força na carga. | Determinação da força que o atuador pode gerar. |
| Venturimeter | Medidor de fluxo de fluido baseado na diferença de pressão. | Pressão em diferentes seções do tubo, velocidade do fluido. | Medição da vazão do fluido. |
| Aspirador de pó | Dispositivo que usa sucção para remover partículas. | Diferença de pressão entre a entrada e a saída, velocidade do ar. | Cálculo da força de sucção do aspirador. |
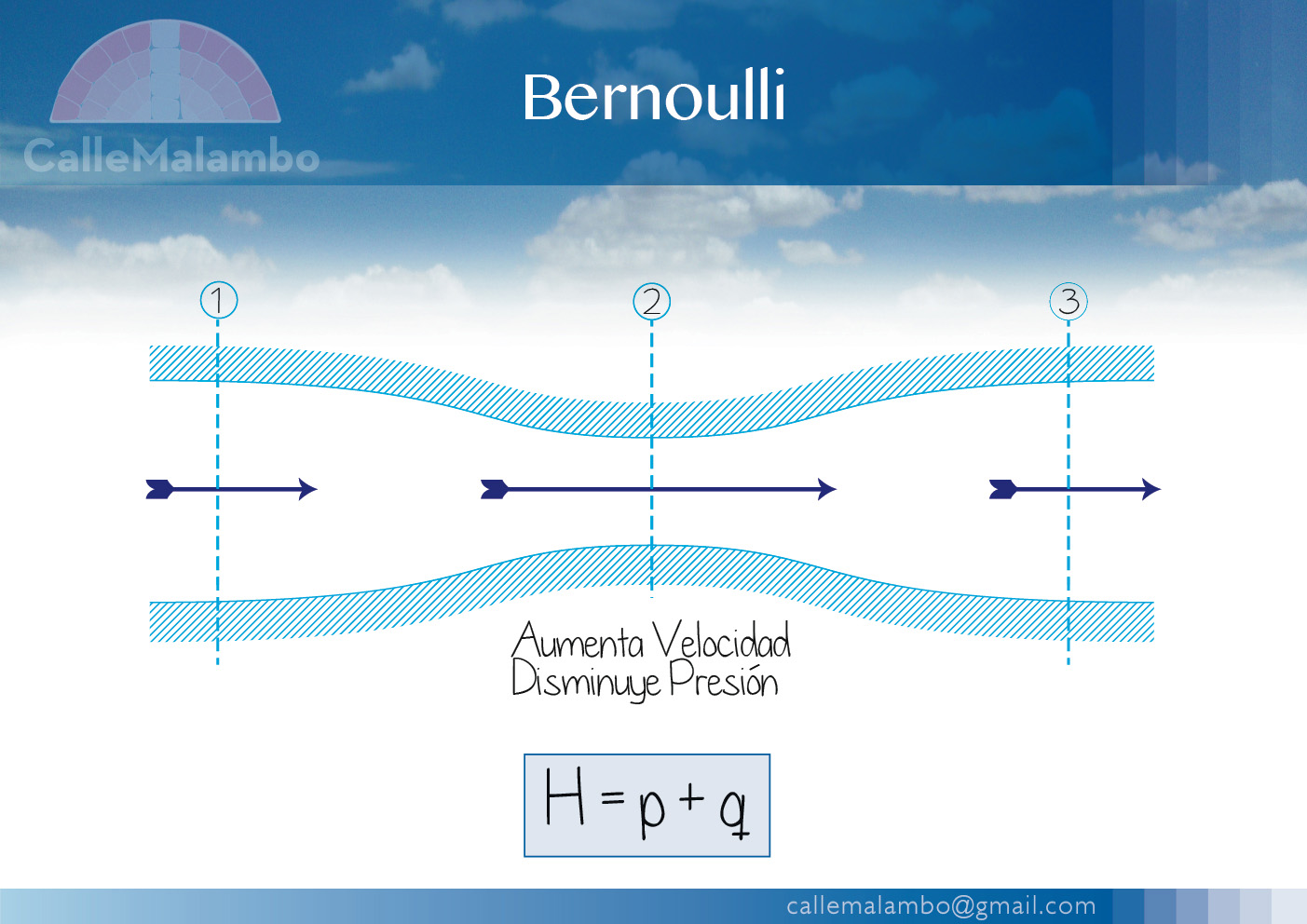
Em aerodinâmica, a equação de Bernoulli explica a geração de sustentação em uma asa de avião. A forma da asa é projetada para acelerar o fluxo de ar sobre a superfície superior, reduzindo a pressão nessa região em comparação com a superfície inferior. Essa diferença de pressão gera uma força resultante para cima, chamada de sustentação.
Em fluidos ideais, a equação de Bernoulli se aplica perfeitamente, pois a viscosidade e a compressibilidade são desprezadas. Em fluidos reais, a viscosidade e a compressibilidade afetam o fluxo, causando perdas de energia e desviando dos resultados previstos pela equação idealizada. É crucial considerar esses fatores em aplicações práticas.
Principais Físicos Envolvidos no Desenvolvimento da Equação
Daniel Bernoulli foi o principal cientista a desenvolver a equação que leva seu nome, publicando suas descobertas em seu livro “Hydrodynamica” em 1738. No entanto, outros cientistas contribuíram para o entendimento dos princípios subjacentes à equação. Leonhard Euler, por exemplo, formalizou a equação em uma forma mais geral, incluindo a influência da gravidade. A evolução da equação de Bernoulli refletiu o progresso na compreensão da mecânica dos fluidos ao longo do tempo.
Exemplos de Cálculos com a Equação de Bernoulli
Um exemplo simples de aplicação da equação em um sistema de tubulação envolve calcular a velocidade da água em um ponto de estrangulamento. Considerando um tubo com diâmetro variável, a equação de Bernoulli pode ser usada para relacionar a velocidade e a pressão em diferentes seções do tubo. A velocidade em um ponto de menor diâmetro será maior devido à conservação de massa (equação da continuidade).
Para determinar a velocidade de um fluido em um ponto específico, a equação de Bernoulli é combinada com a equação da continuidade (A1v1 = A2v2, onde A representa a área da seção transversal do tubo). A aplicação da equação em um aerofólio envolve considerar a diferença de velocidade e pressão entre a superfície superior e inferior, resultando na força de sustentação.
Limitações e Considerações da Equação de Bernoulli
A equação de Bernoulli possui limitações em situações de fluxo turbulento, onde a energia é dissipada devido ao atrito interno. A viscosidade do fluido também afeta a aplicação da equação, causando perdas de energia que não são consideradas na forma idealizada. Fluidos compressíveis também exigem uma abordagem mais complexa, pois a densidade do fluido varia com a pressão.
Ilustrações da Aplicação da Equação
Em um sistema de irrigação, a equação de Bernoulli permite calcular a pressão e a velocidade da água em diferentes pontos do sistema, assegurando um fluxo adequado para a irrigação. A altura da água em reservatórios e a topografia do terreno influenciam na pressão e velocidade da água ao longo do sistema. A equação ajuda a projetar o sistema de forma eficiente e evitar perdas de pressão excessivas.
O projeto da asa de um avião utiliza a equação de Bernoulli para otimizar a geração de sustentação. O perfil aerodinâmico da asa, com sua superfície superior curva e a inferior quase reta, causa uma diferença de velocidade do ar entre as superfícies. Essa diferença de velocidade resulta em uma diferença de pressão, gerando a força de sustentação necessária para o voo.
Um carburador de motor de combustão interna utiliza o princípio de Bernoulli para misturar ar e combustível. O ar é aspirado através de um orifício estreito (venturi), causando uma redução de pressão. Essa redução de pressão permite que o combustível seja aspirado para dentro do fluxo de ar, formando uma mistura combustível-ar que é então queimada no motor. A equação de Bernoulli ajuda a determinar as dimensões do venturi e a taxa de fluxo de combustível para uma mistura adequada.
Qual a diferença entre um fluido ideal e um fluido real na aplicação da equação de Bernoulli?
A equação de Bernoulli é derivada para fluidos ideais (incompressíveis, sem viscosidade e com fluxo irrotacional). Fluidos reais apresentam viscosidade e podem ser compressíveis, o que afeta a precisão da equação, especialmente em situações de fluxo turbulento.
Existem softwares que auxiliam nos cálculos com a equação de Bernoulli?
Sim, diversos softwares de simulação de mecânica dos fluidos (CFD) permitem a modelagem e simulação de escoamentos, incluindo a aplicação da equação de Bernoulli como parte do processo de cálculo. Exemplos incluem ANSYS Fluent e OpenFOAM.
Como a equação de Bernoulli se relaciona com o princípio de conservação de energia?
A equação de Bernoulli expressa a conservação da energia em um fluido em movimento. Ela relaciona a energia cinética, potencial gravitacional e pressão do fluido ao longo de uma linha de corrente.

