Como Calcular A Raiz Do Polinomial Do 1 Grau Exemplos: Imagine um rio fluindo suavemente, seu curso traçado por uma linha invisível – a equação de primeiro grau. A raiz? O ponto exato onde esse rio encontra o mar da solução, o ponto crucial que desvenda o mistério da equação. Vamos desvendar juntos esse enigma matemático, explorando os meandros dos polinômios de primeiro grau e aprendendo a encontrar suas raízes com clareza e precisão.
Descobriremos como os coeficientes “a” e “b” moldam o fluxo da equação, e como, passo a passo, chegamos à solução, revelando a beleza intrínseca da matemática.
Neste percurso, iremos explorar a forma geral de um polinômio de primeiro grau (ax + b = 0), compreendendo o significado dos coeficientes ‘a’ e ‘b’. Veremos exemplos práticos, com coeficientes positivos e negativos, aprendendo a isolar a variável ‘x’ e encontrar a raiz. Aplicaremos esses conceitos a situações reais, modelando problemas do cotidiano como equações de primeiro grau e interpretando a raiz como uma quantidade física, como tempo ou distância.
Finalmente, analisaremos a possibilidade de um polinômio de primeiro grau não possuir raízes reais e o significado geométrico da raiz, visualizando-a como o ponto de interseção com o eixo x em um gráfico.
Introdução aos Polinômios do 1º Grau
Um polinômio do 1º grau, também conhecido como função linear ou equação linear, é uma expressão algébrica que pode ser escrita na forma geral ax + b = 0, onde ‘x’ é a variável, e ‘a’ e ‘b’ são coeficientes constantes, com ‘a’ diferente de zero (a ≠ 0). O coeficiente ‘a’ representa a inclinação da reta que representa graficamente o polinômio, enquanto ‘b’ representa o ponto de interseção com o eixo y.
Forma Geral e Significado dos Coeficientes
A forma geral de um polinômio do 1º grau é ax + b = 0. O coeficiente ‘a’ determina a inclinação da reta; se ‘a’ for positivo, a reta é crescente, e se ‘a’ for negativo, a reta é decrescente. O coeficiente ‘b’ representa o ponto onde a reta intercepta o eixo y (quando x = 0).
Exemplos de Polinômios do 1º Grau
Segue uma tabela com exemplos de polinômios do 1º grau, seus coeficientes e suas raízes (o valor de x que torna a equação verdadeira):
| Exemplo | Coeficiente ‘a’ | Coeficiente ‘b’ | Resultado (raiz) |
|---|---|---|---|
| 2x + 4 = 0 | 2 | 4 | -2 |
| -3x + 6 = 0 | -3 | 6 | 2 |
| x – 5 = 0 | 1 | -5 | 5 |
| 4x = 0 | 4 | 0 | 0 |
Encontrando a Raiz de um Polinômio do 1º Grau: Como Calcular A Raiz Do Polinomial Do 1 Grau Exemplos
A raiz de um polinômio do 1º grau é o valor de ‘x’ que torna a equação igual a zero. Para encontrá-la, isolamos a variável ‘x’ em um dos lados da equação. O processo envolve operações algébricas como adição, subtração, multiplicação e divisão, mantendo o equilíbrio da equação.
Método para Calcular a Raiz
O método para calcular a raiz de um polinômio do 1º grau, ax + b = 0, consiste em isolar o termo com ‘x’ e, em seguida, isolar o ‘x’. Veja os passos:
- Subtraia ‘b’ de ambos os lados da equação: ax = -b
- Divida ambos os lados da equação por ‘a’: x = -b/a
Observe que este método pressupõe que ‘a’ é diferente de zero (a ≠ 0), pois a divisão por zero é indefinida.
Exemplos Numéricos
Vamos resolver alguns exemplos:
- Exemplo 1 (coeficientes positivos): 3x + 6 =
0. Subtraindo 6 de ambos os lados: 3x = –
6. Dividindo por 3: x = -2. - Exemplo 2 (coeficientes negativos): -2x + 8 =
0. Somando 2x em ambos os lados: 8 = 2x. Dividindo por 2: x = 4. - Exemplo 3 (coeficiente ‘b’ igual a zero): 5x =
0. Dividindo por 5: x = 0.
Aplicações Práticas
O cálculo da raiz de um polinômio do 1º grau tem diversas aplicações na vida real, especialmente em situações que podem ser modeladas como relações lineares.
Exemplo Prático: Cálculo de Distância, Como Calcular A Raiz Do Polinomial Do 1 Grau Exemplos
Um carro viaja a uma velocidade constante de 60 km/h. Qual o tempo necessário para percorrer 300 km?
Podemos modelar este problema com a equação d = vt, onde ‘d’ é a distância, ‘v’ é a velocidade e ‘t’ é o tempo. Substituindo os valores, temos: 300 = 60t.
- Isolando ‘t’: t = 300/60
- Calculando: t = 5 horas
Neste caso, a raiz da equação (t = 5) representa o tempo necessário para o carro percorrer a distância especificada.
Considerações Adicionais sobre as Raízes
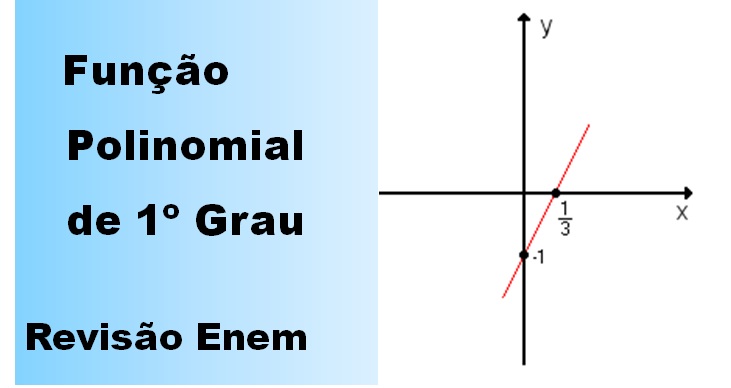
Um polinômio do 1º grau sempre terá uma única raiz real, desde que o coeficiente ‘a’ seja diferente de zero. A raiz representa o ponto onde o gráfico da função linear intercepta o eixo x.
Existência e Significado Geométrico da Raiz
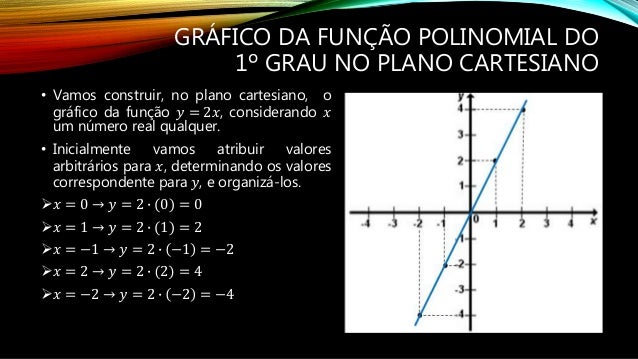
Geometricamente, a raiz de um polinômio do 1º grau representa a coordenada x do ponto onde a reta que representa a função intercepta o eixo x. Em outras palavras, é o ponto (raiz, 0). Se a reta for paralela ao eixo x (a = 0), não haverá intersecção com o eixo x, e portanto, não haverá raiz real.
Imagine um gráfico cartesiano. Uma reta que representa um polinômio do 1º grau sempre cruzará o eixo x em um único ponto. As coordenadas desse ponto são (raiz, 0). A inclinação da reta é definida pelo coeficiente ‘a’, e o ponto de interseção com o eixo y é definido pelo coeficiente ‘b’.
Exercícios Resolvidos
Aqui estão três exercícios resolvidos com diferentes níveis de dificuldade:
| Exercício | Passo a Passo | Resultado | Observações |
|---|---|---|---|
| 5x – 10 = 0 | Adicione 10 em ambos os lados: 5x =
10. Divida por 5 x = 2 |
x = 2 | Equação simples com coeficientes positivos. |
| -4x + 12 = 8 | Subtraia 12 de ambos os lados: -4x = –
4. Divida por -4 x = 1 |
x = 1 | Requer um passo extra para isolar o termo com x. |
| 3(x – 2) = 9 | Distribua o 3: 3x – 6 =
9. Adicione 6 em ambos os lados 3x = 15. Divida por 3 x = 5 |
x = 5 | Envolve a distribuição de um termo antes de isolar x. |

